Конденсаторы

Электрическая емкость

Возьмем два проводника. Они являются нейтральными телами. Расположим их на минимальном расстоянии друг от друга. Разделяет их  воздух ( диэлектрик).  При любом способе заряжения  (трение, магнетизм, химические реакции), один из них приобретает заряд +, другой заряд -.  Между проводниками появляется электрическое поле и возникает разность потенциалов (напряжение).

 

Сильное поле и диэлектрик.

 

В сильном электрическом поле диэлектрик становится проводящим. Наступает так называемый «пробой» диэлектрика: между проводниками проскакивает искра, и они разряжаются. Происходит   переход части заряженных частиц (принято считать, что ими являются электроны), от одного тела к другому. Чем медленнее увеличивается напряжение между проводниками, тем больший заряд можно на них накопить.

Система, состоящая из двух проводников, разделенных диэлектриком, называется конденсатор

 

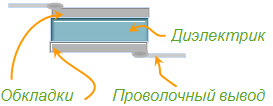
Устройство конденсатора

 

Главным свойством конденсатора является то, что на его электродах могут накапливаться равные по величине и противоположные по знаку электрические заряды.  В начале зарядки (переходный процесс) конденсатор ведет себя как проводник.  Зарядный ток максимален.  Далее, напряжение на обкладках начинает увеличиваться, до насыщения зарядами (сколько позволит емкость). Зарядный ток  при этом постепенно уменьшается и прекращается. В заряженном конденсаторе положительному электроду недостает свободных электронов, а отрицательный имеет избыток. В этом случае между электродами (обкладками) заряженного конденсатора существует определенное напряжение, а в диэлектрике возникает электрическое поле. Напряжение между обкладками, которое возникает при зарядке конденсатора, зависит как от количества электричества, так и от емкости конденсатора. Единица измерения электрической емкости называется Фарада (обозначается Ф или F). Названа в честь Майкла Фарадея.

 

Майкл Фарадей
(1791—1867)
Английский физик, химик и физико-химик,
основоположник учения об электромагнитном поле.
Родился в семье кузнеца.
Открыл электромагнитную индукцию
и сформулировал законы электролиза.

 

  Такая емкость будет у некоторого условного конденсатора, в котором под действием зарядного напряжения 1 вольт накопится заряд в 1 кулон.

 

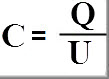
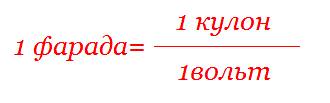
Формула, помогает определить связь между емкостью конденсатора, количеством электричества в нем, и напряжением между его электродами.

Определение:

 

Электроемкость  - способность тела накапливать электрические заряды. Она численно равна заряду, который увеличивает на единицу напряжение между  электродами.

 

Величина 1 Фарада, очень большая. Для ее получения потребовались бы обкладки диаметром несколько десятков километров, при расстоянии между ними 1мм. Земной шар имеет емкость примерно 0,00070 Ф.

В современной аппаратуре, используют более мелкие величины:

 

Обозначается конденсатор буквой С. , то есть емкость 1 Фарад

 

Маленькая задачка

Давайте определим напряжение, возникающее между электродами (обкладками) конденсатора емкостью 50 мкф, если зарядить его зарядом в 0,005 кулона.

 Решение

Воспользуемся формулой определения емкости,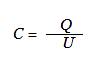

и узнаем требуемую величину.Получается, что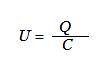

Подставим числовые значения.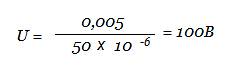

 

Емкость конденсатора зависит от площади обкладок, расстояния между ними и диэлектрической проницаемости диэлектрика (число, которое показывает, во сколько раз возрастает емкость конденсатора). С увеличением площади обкладок увеличивается и емкость конденсатора, но это приводит к увеличению его размеров. При уменьшении расстояния между обкладками разноименные заряды оказываются ближе друг к другу, электрическое поле между электродами становится более интенсивным. Сближать обкладки можно только до определенного расстояния. Иначе, увеличивается опасность короткого замыкания (пробой конденсатора). Поэтому, производители идут более простым путем, экспериментируют с диэлектриками. Емкость простого плоского конденсатора, с одинаковыми обкладками, вычисляется по формуле:

 

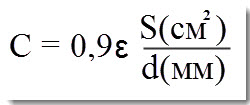
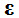- относительная диэлектрическая проницаемость диэлектрика.

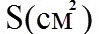- площадь одной из обкладок.

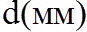- расстояние между обкладками..

 

Диэлектрики, используемые в конденсаторах, должны иметь большую электрическую прочность (выдерживать большое напряжение), и иметь небольшие потери при работе на высоких частотах .

 

Конденсатор и постоянный ток.

При подключении конденсатора к источнику тока, на обкладке со знаком  (-) происходит накопление зарядов, с противоположной обкладки заряды уходят.

 

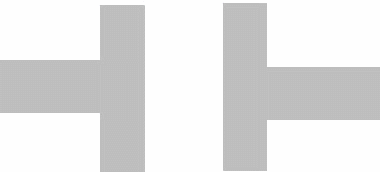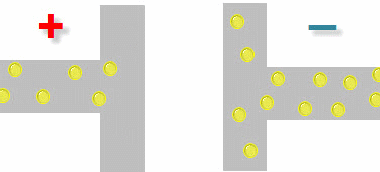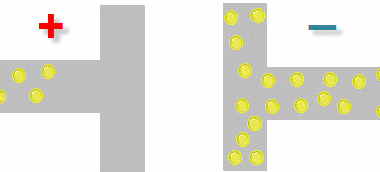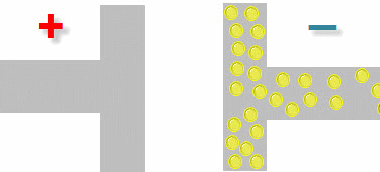
Накопление зарядов. Постоянный ток.

 

Разберем работу конденсатора в цепи постоянного тока. Помощники: лампочка, батарейка и конденсатор.

При замыкании цепи некоторое время протекает зарядный ток. Он протекает, пока заряжается конденсатор (переходный процесс). Зарядка  происходит постепенно. Как только мы подсоединим конденсатор к источнику тока, напряжение между обкладками будет равно нулю. Ток максимален (зарядный ток).

Далее, напряжение на емкости начинает увеличиваться.

 

При этом общее напряжение в цепи и зарядный ток уменьшаются. Когда напряжение на конденсаторе достигает примерно от 95 до 97% приложенного напряжения источника тока, или когда зарядный ток достигает только 3-5% тока в первый момент включения, переходный процесс завершается.

Конденсатор и постоянный ток.

Время зарядки - разрядки конденсатора(переходный процесс). Продолжительность переходного процесса определяется формулой

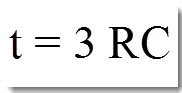
t -время (секунды), С - емкость (фарад), R - сопротивление цепи (оМ). Учитываем, что в сопротивление цепи входит сопротивление источника тока. В практике вычислений, RC - постоянная времени цепи, но она не равна времени полного заряда и разряда конденсатора. Для простоты изложения введен множитель 3. Он указывает, что для полной зарядки - разрядки конденсатора требуется время в три раза больше времени постоянной цепи RC (множитель варьируется от 3 до 5).

 

Маленькая задачка

Давайте определим за какое время зарядится конденсатор емкостью С  = 1000 мкф, через лампочку сопротивлением R =17 оМ.

 

Решение

Подставим значения в формулу

t=3x17x1000x0.000001=0.05c

 

При подключении  нагрузки (сопротивления) R= 500 кОм , переходный процесс будет длиться  1500 с (25 мин). В данном примере, мы намеренно взяли большую емкость и меняли сопротивление.

Вывод

Большая емкость через маленькое сопротивление заряжается быстрее. Та же  емкость, через большое сопротивление, заряжается дольше. Разрядка конденсатора  сопровождается похожими  явлениями и вычисляется этой же формулой.

 

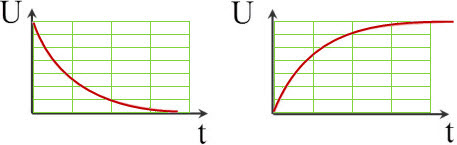
Разрядка конденсатора              Зарядка конденсатора

 

Конденсатор и переменный ток.

Емкостное сопротивление (Хс). Переменный ток в проводниках представляет собой колебательное движение электронов то в одном, то в другом направлении. Если к источнику переменного тока подключить конденсатор, то его обкладки будут периодически заряжаться и разряжаться электронами. Процесс проходит при  увеличении и уменьшении амплитуды переменного тока. Движение электронов от одной обкладки к другой представляет собой ток.

 

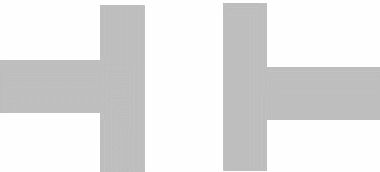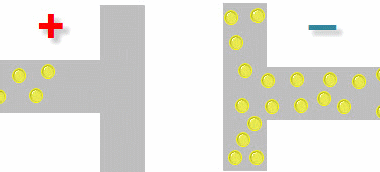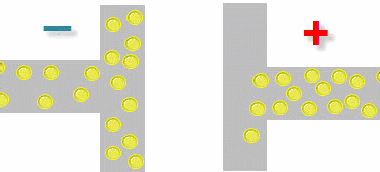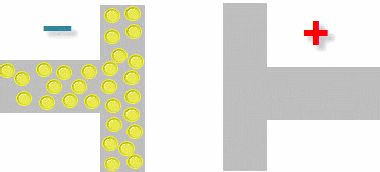
Накопление зарядов. Переменный ток.

 

Переменный ток, текущий через резистор, изменяется под действием напряжения или сопротивления цепи. В последовательной и параллельной цепи переменного тока приложенное напряжение, общий ток и токи в отдельных ветвях находятся в фазе. Вычисляются по закону Ома для постоянной цепи.

Синусоиды тока и напряжения проходят через нуль и принимают максимальные значения в одни и те же моменты времени. То есть сопротивление в эти промежутки, будет активно. Однако эти две синусоиды имеют разные амплитуды, поскольку представляют различные величины, измеряемые в различных единицах.

 

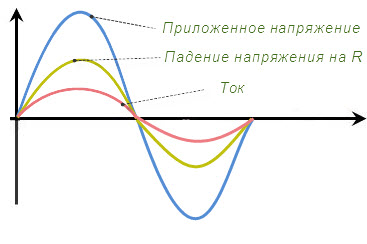
Резистивная цепь. Максимум напряжения и тока наступает одновременно.

 

В большинстве расчетов используются эффективные или действующие значения. Они рассматриваются как эквивалентное значение определенной величины при постоянном токе. Нужно отметить, что в цепях переменного тока, мощность потребляется точно так же, как и в цепях постоянного тока. Иначе обстоит дело с конденсатором, в цепи переменного тока (емкостная цепь). Ток опережает приложенное напряжение, и находятся они не в фазе. Поэтому, сопротивление конденсатора реактивно. Приложенное напряжение постоянно изменяется, вынуждая конденсатор заряжаться и разряжаться.  

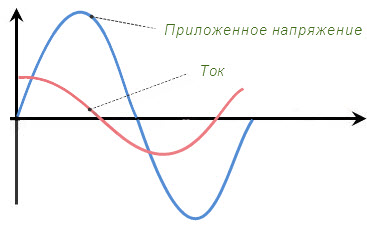
Емкостная цепь. Максимум напряжения и тока не наступает одновременно.

 

После того как конденсатор зарядится, напряжение на его обкладках противодействует любому изменению приложенного напряжения. Противодействие, которое конденсатор оказывает приложенному переменному напряжению, называется емкостным сопротивлением. Вычисляется по формуле:

 

 

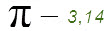
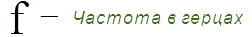
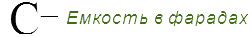
Маленькая задачка

Найдем емкостное сопротивление конденсатора Хс, подключенного к осветительной сети с  частотой 50 Гц, емкостью  5 мкф.

 

Решение

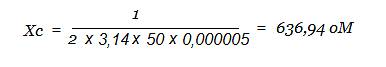
С увеличением частоты, емкостное сопротивление будет уменьшаться. Соответственно, резко возрастет ток. Уменьшение частоты, увеличивает сопротивление. Ток падает. Проще и быстрее, емкостное сопротивление, определяется при помощи уже знакомой номограммы. Конечно, при визуальном определении будут неточности. Этот способ справедлив, если считать мешает "матушка" лень. Найдем Хс, при частоте 100 кГц, на конденсаторе 100 пф. Проведем от деления 100 кГц шкалы "Частота" вертикальную линию (пунктир), до оранжевой линии  "Емкость"  100 пф. От точки их пересечения, проведем горизонтальную линию до шкалы "Сопротивление". Как видно из рисунка, сопротивление больше 10 КоМ.

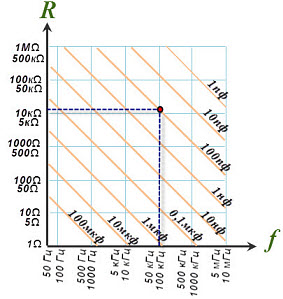
Номограмма для определения емкостного сопротивления.

 

Разобравшись с емкостным сопротивлением, мы можем смело записать закон Ома для переменного тока,  протекающего через конденсатор.

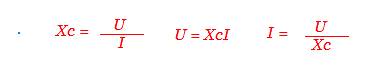
Эти зависимости проявляются тогда, когда конденсатор подключен к переменному синусоидальному напряжению.

Маленькая задачка

Какое приложенное напряжение будет у конденсатора, емкостью 1 мкф, на частоте 100 Гц, если протекает ток 0,6 А.

 Решение

Подставляем исходные значения

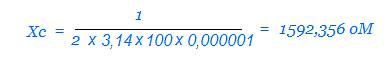
Округляем в большую сторону Хс = 1,6 КоМ, и находим приложенное напряжение.

E=1600x0.6=960 вольт

 

 

Далее материалы по теме

 

Параметры и обозначение конденсаторов

Цифробуквенная маркировка конденсаторов

Соединение конденсаторов

Цветовая маркировка конденсаторов